Parallel Enhanced Whale Optimization Algorithm In CUDA By Bevan Stanely https://bevs.xyz/
Please press s for speaker notes!
Rely on simple concepts No need for gradient information Can bypass local optima Useful across wide range of problems Motivation
Popular in Engineering applications because-
Stochastic hence need random numbers
Exploratory and Exploitatory phases
Whale Optimization Algorithm (WOA) Inspired by the bubble-net feeding behavior of humpback whales Drawbacks Low exploration ability Slow convergence speed Sticking with local solution easily. WOAmM Enhanced Whale Optimization Algorithm
Addresses these drawbacks
We want to develop a Parallel WOAmM with SpeedUPs in GPU
Quality and size of RNGs Data dependencies GPU RNGs have lower quality host implementations are bulky and slow Sequential algorithms have data dependencies which aid in parallelization Enhanced Whale Optimization Algorithm (WOAmM) Note:
Hybrid algorithm with
Two components
mSOS Modified Mutualism phase of the symbiotic organism search (mSOS) algorithm
$$
P^{(k+1)}_i= P^{(k)}_i+rnd\cdot(P_s - MV\cdot BF1)
$$
$$
P^{(k+1)}_r= P^{(k)}_n+rnd\cdot(P_s - MV\cdot BF2)
$$
WOA
Randomly searching the prey Encircling the prey Bubble-net attacking strategyAssume current best solution to be optimum and attack it How to Parallelise? Model individuals as GPU threads Intra-warp Communication with Butterfly reduction Avoiding Warp Divergence Random Numbers for ( each thread in warp ) do {
while ( k < max_iter ){
mSOS ();
WOA ();
k ++ ;
}
}
return best solution
We wanted to capitalize the warp level primitives, and hence fixed the population size to the warp size
Direct communication to communicate position vectors
Threads in a warp execute instructions in sync at every instant
We had 3 data dependent if else conditions
Intra warp communication is faster than shared memory If else conditions have been avoided by using pointer arrays Random numbers: Device RNGs and Host RNG Experiment Parameters Range RNG MTGP32,MRG32k3a,Philox_4x32_10 Iterations {30,100,300} Blocks {1,2,4,6} Functions {Sphere,Rosenbrock,Rastrigin,Griewank}
Function Properties:
Dimension = 30 Optimum Value = 0 Sequential algorithm used Mersanne Twister 64 bit RNG
We have ignored the RNG initiation times for the experiments and focussed on computation times and memory copy costs.
It is hence suitable for bulk optimizations, so that reuse of state is possible.
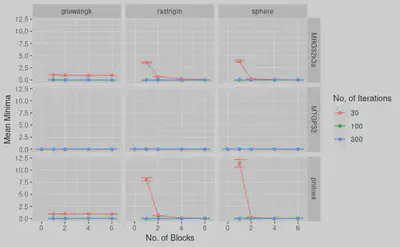
The parallel implementation across all parameters was compared with sequential algorithm for their optimization quality.
Ive ignored rosenbrock because it did really bad for single block
The GPU RNGs did bad in single block and 30 iterations
Increasing block size had some effect upto 4 blocks
But increasing iterations were more effective
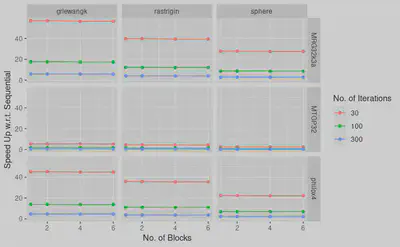
MRG32k3a with 100 iterations and 2 blocks appears to give best results The parallel implementation across all parameters was compared with sequential algorithm for their speedUp.
The speed up remains constant when increasing number of blocks
Future Direction Search for better GPU RNGs Running multiple instances of Parallel WOAmM within a single block and syncing the best solution across all instances halfway through the optimization. Chaotic Maps instead of RNG